5. Vectors
c. Scalar Multiplication
In discussing vectors, we normally specify a vector as an ordered pair of components. However, there is a second notation which involves two special vectors: \(\hat\imath\) and \(\hat\jmath\).
5. \(\hat\imath\hat\jmath\) Notation
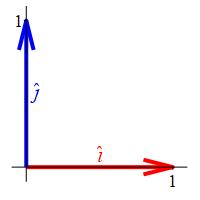
There exist two special unit vectors that point in the directions of the
positive \(x\)- and \(y\)-axes. They are:
\[
\hat\imath=\left\langle1,0\right\rangle \quad \text{and} \quad
\hat\jmath=\left\langle0,1\right\rangle
\]
They are called the standard coordinate vectors
or the standard basis vectors.
Notice that we put hats over these vectors because they are in fact
unit vectors.
What happens if we take an arbitrary linear combination of \(\hat\imath\) and \(\hat\jmath\) with coefficients \(a\) and \(b\)? \[\begin{aligned} a\hat\imath+b\hat\jmath &=a\left\langle1,0\right\rangle+b\left\langle0,1\right\rangle \\ &=\left\langle a,0\right\rangle+\left\langle0,b\right\rangle =\left\langle a,b\right\rangle \end{aligned}\] We get the vector \(\left\langle a,b\right\rangle\). Turning this around, we can express any vector \(\vec v\) in terms of \(\hat\imath\) and \(\hat\jmath\): \[ \vec v=\left\langle v_1,v_2\right\rangle =v_1\hat\imath+v_2\hat\jmath \]
For example, the vector \(\vec v=\left\langle3,-2\right\rangle\) can be written as \(\vec v=3\hat\imath-2\hat\jmath\).
The ordered pair notation, \(\vec v=\left\langle v_1,v_2\right\rangle\), and the \(\hat\imath\,\hat\jmath\) notation, \(\vec v=v_1\hat\imath+v_2\hat\jmath\), can be used interchangably. For some purposes one or the other may be more useful.
You need to be able to go back and forth as needed.
Write the vector \(\vec a=\left\langle5,-3\right\rangle\) in \(\hat\imath\,\hat\jmath\) notation.
\(\vec a=5\hat\imath-3\hat\jmath\)
Write the vector \(\vec a=-4\hat\imath+2\hat\jmath\) in ordered pair notation.
\(\vec a=\left\langle-4,2\right\rangle\)
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum